My sincere thanks to the team of warriors who are combating, successfully, in containing the spread of COVID-19.
Despite the team has its own systemic limitations (from the availability of testing equipments, facilities, skilled testers, time to transport the collected samples from the patients, duration of testing and many other constraints) it continues to increase the number of tests performed. I feel it is key for breaking the chain of disease transmission.
I’m sincerely thankful to the government and the various data providers for the regular updates.
As I mentioned earlier in the newsletter the reported cases of the COVID-19 are just our observations. It is not the count of the actual number of people infected by the disease.
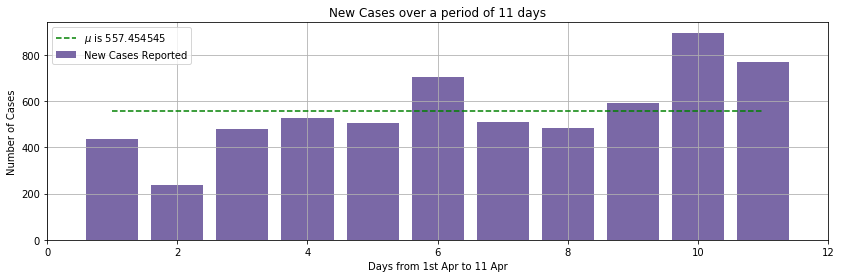
We collected the count of new cases, of COVID-19 diseases, per day from Apr 1 to Apr 11. The source https://en.wikipedia.org/wiki/2020_coronavirus_pandemic_in_India
A bar graph of the observation is here for your reference.
Motive
Our intention is not to exactly predict the count of how many people will be infected in the next few days. We all pray for it to be zero. I’m not going to do that in this post.
We do not want an overconfident prediction framework that just relies on the data and provides a point estimate about the future. Besides, we can’t afford to wait for a large dataset to perform the prediction in leisure.
The Bayesian inference framework is our choice because it supports us to incorporate our prior, optimistic, beliefs and at the same time helps us to align our inferences based on new evidences. The most significant feature of Bayesian inference is its ability to expose the degree of uncertainties in our predictions. The philosophy is Courage and fail-fast.
I believe that the number of cases will not grow exponentially for various reasons.
- Our government has acted wisely in a timely manner to check the disease transmission.
- We gradually understand the importance of staying at home though we were little disobedient during the first few days.
- We have strong immune.
The framework allows us to incorporate these beliefs as Priors.
At the same time I don’t want to be super optimistic and be a daydreamer. I always align my hypothesis in the Likelihood of new evidence made available to me. The new evidence may be either an increase or a decrease in the number of new cases reported on a day.
Of course, If you have a different belief, nothing stops you from incorporating your prior beliefs until our beliefs are washed away by the new evidences.
So the priors and the likelihoods are the key ingredients of the Bayesian framework. Our endeavor here is, use the prior and the likelihood to calculate the posterior probability – The probability of the hypothesis given the observed evidence.
Fitting the Model
Poisson distribution is appropriate to model the number of times an event occurs in an interval of time or space. The daily count of patients tested positive for the disease forms a discrete probability distribution and can be perfectly modeled with the Poisson distribution.
The probability of observing k patients in an interval can be calculated using this famous probability mass function equation of Poisson distribution.

Where ƛ is the rate parameter that drives the Poisson distribution and is unfortunately hidden from us, because of multiple possible mappings between the rate parameter and the set of data.
An interesting property of the Poisson distribution is its expected value equals this rate parameter – ƛ. Hence the distribution of latent ƛ is the representation of the risk ahead.
The rest of the exercise is to infer the distribution of the rate parameters, ƛs, given the observed patient data.
More precisely, exploring the posterior probabilities of this rate parameter given the observed data is the ultimate aim of our exercise.
Modeling
We will use PyMC3, which is a Python library for performing Bayesian analysis and to obtain the posterior distribution of ƛs.
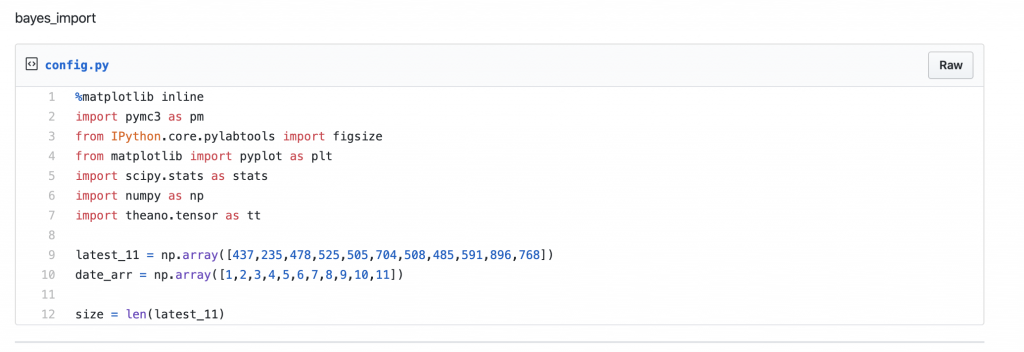
Let us start by importing the required python library components and create an array to hold the daily count of infected people as sourced from COVID-19 Wiki.
[gist https://gist.github.com/krsmanian1972/533d45fdbdddc8d4aead1a739b912cf9 /]
As stated earlier, our aim is to obtain the distribution of ƛs. Let us work backward which is a common pattern in probabilistic programming to explore the distribution.
- We have our observations captured in the array latest_11. The observations are an ingredient to model the Poisson distribution.
- The Poisson distribution is driven by a distribution of ƛs.
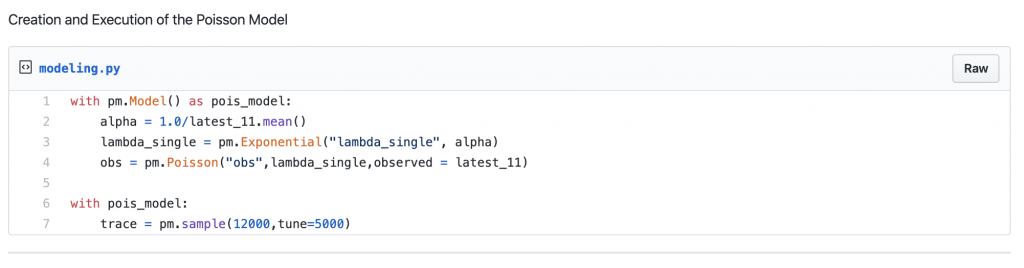
- As we do not know the distribution of lambdas, we believe that it can be randomly sampled and proposed from an Exponential distribution. This is the first prior belief.
- Now we encountered the next unknown. The Exponential distribution needs a parameter, alpha, to propose values for the probable lambdas.
- Alpha is the hyper-parameter, which we believe to have an initial value which is an inverse of the mean of observation. This is our second belief.
[gist https://gist.github.com/krsmanian1972/4f5f86406302e4e480c02866dbaca9d3 /]
Result
Inference
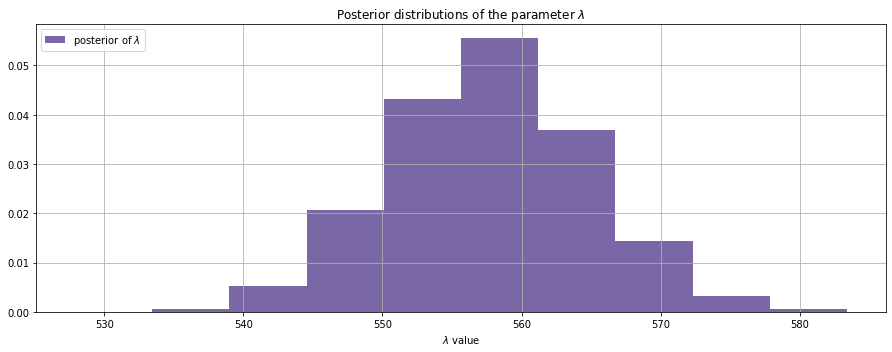
Remember that the number of patients on a day is Poisson distributed. In a Poisson distribution the expected value on a particular day is the posterior value of ƛ.
Now we have a distribution instead of a point-estimate. Hence we can expect any count from 540 to 580 in a day but should admit the uncertainty.
Though the priors for the ƛ have been randomly sampled from an exponential distribution, we could infer that it is not likely for the number of cases to grow exponentially, as of now, given the data we received.
I acknowledge that our inference will be very unstable with such a small set of data. I’m fine with that.
I leave it to the readers to perform a change-point analysis after 5 days from today. I hope to see a mixed Poisson distribution in the observed data with reduced lambda patterns.
Next
The PyMC3 Library uses a family of algorithm called Markov Chain Monte Carlo methods- MCMC to generate the posterior distribution. In our next post, we will code one such algorithm using RUST lang
Artifacts
You can access the Jupyter Notebook I’ve used for the analysis from here https://github.com/krsmanian1972/bayes/blob/master/COVID-19-India.ipynb.
Probabilistic-Programming-and-Bayesian-Methods-for-Hackers is a fantastic book to appreciate the Bayesian framework and techniques in greater depth from programmers’ point-of-view.
Thank you.

